Los coeficientes de correlación son indicadores de la fuerza de la relación lineal entre dos variables diferentes, xey. Un coeficiente de correlación lineal mayor que cero indica una relación positiva. Un valor menor que cero significa una relación negativa. Finalmente, un valor de cero indica que no hay relación entre las dos variables xey. Este artículo explica la importancia del coeficiente de correlación lineal para los inversores, cómo calcular la covarianza de las acciones y cómo los inversores pueden utilizar la correlación para predecir el mercado.

CONSEJOS CLAVE:

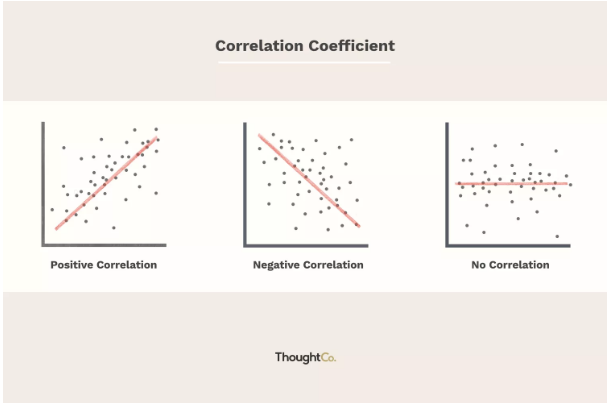
• Los coeficientes de correlación se utilizan para medir la fuerza de la relación lineal entre dos variables.
• Un coeficiente de correlación mayor que cero indica una relación positiva, mientras que un valor menor que cero significa una relación negativa.
• Un valor de cero indica que no hay relación entre las dos variables que se comparan.
• Una correlación negativa, o correlación inversa, es un concepto clave en la creación de carteras diversificadas que pueden resistir mejor la volatilidad de la cartera.
• Calcular el coeficiente de correlación requiere mucho tiempo, por lo que los datos a menudo se conectan a una calculadora, computadora o programa de estadísticas para encontrar el coeficiente.

Entendiendo la correlación

El coeficiente de correlación (ρ) es una medida que determina el grado en que se asocia el movimiento de dos variables diferentes. El coeficiente de correlación más común, generado por la correlación producto-momento de Pearson, se utiliza para medir la relación lineal entre dos variables. Sin embargo, en una relación no lineal, este coeficiente de correlación puede no ser siempre una medida adecuada de dependencia.

El rango posible de valores para el coeficiente de correlación es de -1,0 a 1,0. En otras palabras, los valores no pueden exceder 1.0 ni ser menores que -1.0. Una correlación de -1,0 indica una correlación negativa perfecta y una correlación de 1,0 indica una correlación positiva perfecta. Si el coeficiente de correlación es mayor que cero, es una relación positiva. Por el contrario, si el valor es menor que cero, es una relación negativa. Un valor de cero indica que no existe relación entre las dos variables.

Importante: al interpretar la correlación, es importante recordar que el hecho de que dos variables estén correlacionadas no significa que una cause la otra.

Correlación y mercados financieros

En los mercados financieros, el coeficiente de correlación se utiliza para medir la correlación entre dos valores. Por ejemplo, cuando dos acciones se mueven en la misma dirección, el coeficiente de correlación es positivo. Por el contrario, cuando dos acciones se mueven en direcciones opuestas, el coeficiente de correlación es negativo.

Si el coeficiente de correlación de dos variables es cero, no existe una relación lineal entre las variables. Sin embargo, esto es solo para una relación lineal. Es posible que las variables tengan una fuerte relación curvilínea. Cuando el valor de ρ es cercano a cero, generalmente entre -0,1 y +0,1, se dice que las variables no tienen relación lineal (o una relación lineal muy débil).

Por ejemplo, suponga que se observan los precios del café y las computadoras y se encuentra que tienen una correlación de + 0008. Esto significa que no existe correlación o relación entre las dos variables.

Calculando ρ

La covarianza de las dos variables en cuestión debe calcularse antes de poder determinar la correlación. A continuación, se requiere la desviación estándar de cada variable. El coeficiente de correlación se determina dividiendo la covarianza por el producto de las desviaciones estándar de las dos variables.

La desviación estándar es una medida de la dispersión de datos de su promedio. La covarianza es una medida de cómo dos variables cambian juntas. Sin embargo, su magnitud no tiene límites, por lo que es difícil de interpretar. La versión normalizada de la estadística se calcula dividiendo la covarianza por el producto de las dos desviaciones estándar. Este es el coeficiente de correlación.

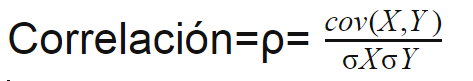
Correlacion positiva

Una correlación positiva, cuando el coeficiente de correlación es mayor que 0, significa que ambas variables se mueven en la misma dirección. Cuando ρ es +1, significa que las dos variables que se comparan tienen una relación positiva perfecta; cuando una variable se mueve hacia arriba o hacia abajo, la otra variable se mueve en la misma dirección con la misma magnitud.

Cuanto más cercano esté el valor de ρ a +1, más fuerte será la relación lineal. Por ejemplo, supongamos que el valor de los precios del petróleo está directamente relacionado con los precios de los billetes de avión, con un coeficiente de correlación de +0,95. La relación entre los precios del petróleo y las tarifas aéreas tiene una correlación positiva muy fuerte ya que el valor se acerca a +1. Entonces, si el precio del petróleo baja, las tarifas aéreas también disminuyen, y si el precio del petróleo aumenta, también lo hacen los precios de los billetes de avión.

En el cuadro a continuación, comparamos uno de los bancos más grandes de EE. UU., JPMorgan Chase & Co. (JPM), con Financial Select SPDR Exchange Traded Fund (ETF) (XLF) .Como puede imaginar, JPMorgan Chase & Co. debería tener una correlación positiva con la industria bancaria en su conjunto. Podemos ver que el coeficiente de correlación se encuentra actualmente en 0.98, lo que indica una fuerte correlación positiva. Una lectura superior a 0,50 normalmente indica una correlación positiva.

Coeficiente de correlación JPM y XLF

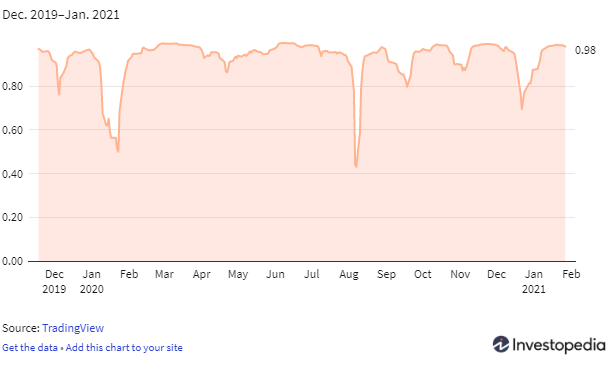
Comprender la correlación entre dos acciones (o una sola acción) y su industria puede ayudar a los inversores a evaluar cómo se negocia la acción en relación con sus pares. Todos los tipos de valores, incluidos bonos, sectores y ETF, se pueden comparar con el coeficiente de correlación.

Correlación negativa

Una correlación negativa (inversa) ocurre cuando el coeficiente de correlación es menor que 0. Esto es una indicación de que ambas variables se mueven en la dirección opuesta. En resumen, cualquier lectura entre 0 y -1 significa que los dos valores se mueven en direcciones opuestas. Cuando ρ es -1, se dice que la relación está perfectamente correlacionada negativamente. En resumen, si una variable aumenta, la otra variable disminuye con la misma magnitud (y viceversa). Sin embargo, el grado en el que dos valores están correlacionados negativamente puede variar con el tiempo (y casi nunca están exactamente correlacionados todo el tiempo).

Ejemplos de correlación negativa

Por ejemplo, suponga que se realiza un estudio para evaluar la relación entre la temperatura exterior y las facturas de calefacción. El estudio concluye que existe una correlación negativa entre los precios de las facturas de calefacción y la temperatura exterior. El coeficiente de correlación se calcula en -0,96. Esta fuerte correlación negativa significa que a medida que desciende la temperatura exterior, los precios de las facturas de calefacción aumentan (y viceversa).

Cuando se trata de invertir, una correlación negativa no significa necesariamente que deban evitarse los valores. El coeficiente de correlación puede ayudar a los inversores a diversificar su cartera al incluir una combinación de inversiones que tienen una correlación negativa o baja con el mercado de valores. En resumen, cuando se reduce el riesgo de volatilidad en una cartera, a veces se atraen los opuestos.

Por ejemplo, suponga que tiene una cartera equilibrada de $ 100,000 que se invierte un 60% en acciones y un 40% en bonos. En un año de sólido desempeño económico, el componente de acciones de su cartera podría generar un rendimiento del 12%, mientras que el componente de bonos podría rendir un -2% porque las tasas de interés están subiendo (lo que significa que los precios de los bonos están bajando). Por lo tanto, el rendimiento general de su cartera sería del 6,4% ((12% x 0,6) + (-2% x 0,4). El año siguiente, a medida que la economía se desacelera notablemente y las tasas de interés bajan, su cartera de acciones podría generar -5 % mientras que su cartera de bonos puede devolver un 8%, lo que le da un rendimiento total de la cartera del 0,2%.

¿Y si, en lugar de una cartera equilibrada, su cartera fuera 100% de acciones? Utilizando los mismos supuestos de rendimiento, su cartera de capital total tendría un rendimiento del 12% en el primer año y del -5% en el segundo año. Estas cifras son claramente más volátiles que las rentabilidades de la cartera equilibrada del 6,4% y el 0,2%.

Coeficiente de correlación lineal

El coeficiente de correlación lineal es un número calculado a partir de datos dados que mide la fuerza de la relación lineal entre dos variables, xey. El signo del coeficiente de correlación lineal indica la dirección de la relación lineal entre xey. Cuando r (el coeficiente de correlación) está cerca de 1 o -1, la relación lineal es fuerte; cuando está cerca de 0, la relación lineal es débil.

Incluso para conjuntos de datos pequeños, los cálculos del coeficiente de correlación lineal pueden ser demasiado largos para realizarlos manualmente. Por lo tanto, los datos a menudo se conectan a una calculadora o, más probablemente, a una computadora o programa de estadísticas para encontrar el coeficiente.

El coeficiente de Pearson

Tanto el cálculo del coeficiente de Pearson como la regresión lineal básica son formas de determinar cómo se relacionan linealmente las variables estadísticas. Sin embargo, los dos métodos difieren. El coeficiente de Pearson es una medida de la fuerza y ​​la dirección de la asociación lineal entre dos variables sin supuesto de causalidad. El coeficiente de Pearson muestra correlación, no causalidad. Los coeficientes de Pearson van de +1 a -1, donde +1 representa una correlación positiva, -1 representa una correlación negativa y 0 representa ninguna relación.

La regresión lineal simple describe la relación lineal entre una variable de respuesta (indicada por y) y una variable explicativa (indicada por x) utilizando un modelo estadístico. Los modelos estadísticos se utilizan para hacer predicciones.

Consejo: simplifique la regresión lineal calculando la correlación con software como Excel.

En finanzas, por ejemplo, la correlación se utiliza en varios análisis, incluido el cálculo de la desviación estándar de la cartera. Debido a que requiere mucho tiempo, la correlación se calcula mejor con un software como Excel. La correlación combina conceptos estadísticos, a saber, varianza y desviación estándar. La varianza es la dispersión de una variable alrededor de la media y la desviación estándar es la raíz cuadrada de la varianza.

Encontrar correlación con Excel

Existen varios métodos para calcular la correlación en Excel. La más simple es obtener dos conjuntos de datos uno al lado del otro y usar la fórmula de correlación incorporada:

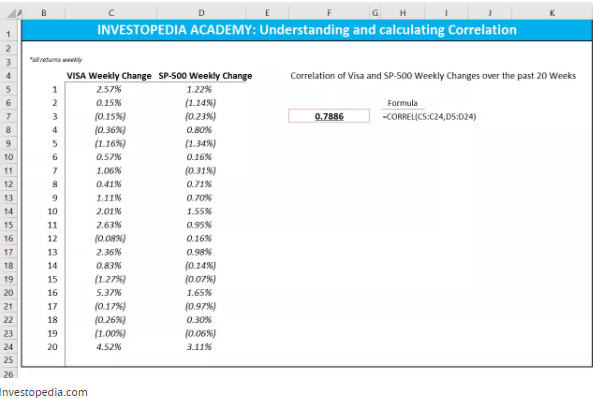
Si desea crear una matriz de correlación en un rango de conjuntos de datos, Excel tiene un complemento de Análisis de datos que se encuentra en la pestaña Datos, en Analizar.

Seleccione la tabla de devoluciones. En este caso, nuestras columnas están tituladas, por lo que queremos marcar la casilla “Etiquetas en la primera fila”, para que Excel sepa tratarlas como títulos. Luego, puede optar por imprimir en la misma hoja o en una nueva hoja.

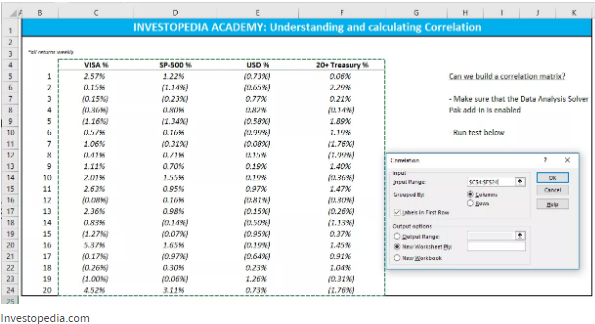
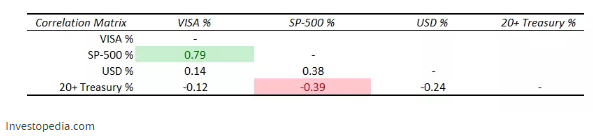
Una vez que presiona Enter, los datos se crean automáticamente. Puede agregar texto y formato condicional para limpiar el resultado.

Preguntas frecuentes sobre el coeficiente de correlación lineal

¿Qué es el coeficiente de correlación lineal?

El coeficiente de correlación lineal es un número calculado a partir de datos dados que mide la fuerza de la relación lineal entre dos variables, xey.

¿Cómo se encuentra el coeficiente de correlación lineal?

La correlación combina varios conceptos estadísticos importantes y relacionados, a saber, varianza y desviación estándar. La varianza es la dispersión de una variable alrededor de la media y la desviación estándar es la raíz cuadrada de la varianza.

La formula es:

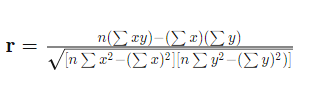
La computación es demasiado larga para hacerla manualmente y el software, como Excel, o un programa de estadística, son herramientas que se utilizan para calcular el coeficiente.

¿Qué se entiende por correlación lineal?

El coeficiente de correlación es un valor entre -1 y +1. Un coeficiente de correlación de +1 indica una correlación positiva perfecta. A medida que aumenta la variable x, aumenta la variable y. A medida que la variable x disminuye, la variable y disminuye. Un coeficiente de correlación de -1 indica una correlación negativa perfecta. A medida que aumenta la variable x, la variable z disminuye. A medida que la variable x disminuye, la variable z aumenta.

¿Cómo se encuentra el coeficiente de correlación lineal en una calculadora?

Se requiere una calculadora gráfica para calcular el coeficiente de correlación. Statology proporciona las siguientes instrucciones

Paso 1: active los diagnósticos

Solo necesitará hacer este paso una vez en su calculadora. Después de eso, siempre puede comenzar en el paso 2 a continuación. Si no hace esto, r (el coeficiente de correlación) no aparecerá cuando ejecute la función de regresión lineal.

Presione [2nd] y luego [0] para ingresar al catálogo de su calculadora. Desplácese hasta que vea “diagnosticsOn”.

Presione enter hasta que la pantalla de la calculadora diga “Done”.

Es importante repetir esto: nunca más tendrá que hacer esto a menos que reinicie su calculadora.

Paso 2: Ingrese los datos

Ingrese sus datos en la calculadora presionando [STAT] y luego seleccionando 1: Edit. Para facilitar las cosas, debe ingresar todos sus “datos x” en L1 y todos sus “datos y” en L2.

Paso 3: ¡Calcule!

Una vez que tenga sus datos, ahora irá a [STAT] y luego al menú CALC en la parte superior. Finalmente, seleccione 4: LinReg y presione enter.

¡Eso es! ¡Terminaste! Ahora puede simplemente leer el coeficiente de correlación directamente desde la pantalla (su r). Recuerde, si r no aparece en su calculadora, entonces los diagnósticos deben estar activados. Este es también el mismo lugar en la calculadora donde encontrará la ecuación de regresión lineal y el coeficiente de determinación.

La línea de fondo

El coeficiente de correlación lineal puede ser útil para determinar la relación entre una inversión y el mercado general u otros valores. A menudo se utiliza para predecir los rendimientos del mercado de valores. Esta medición estadística es útil de muchas maneras, particularmente en la industria financiera. Por ejemplo, puede ser útil para determinar qué tan bien se está comportando un fondo mutuo en comparación con su índice de referencia, o puede usarse para determinar cómo se comporta un fondo mutuo en relación con otro fondo o clase de activos. Al agregar un fondo mutuo bajo o correlacionado negativamente a una cartera existente, se obtienen beneficios de diversificación.