La Regla del 72 es una fórmula rápida y útil que se usa popularmente para estimar el número de años necesarios para duplicar el dinero invertido a una tasa de rendimiento anual determinada.

Si bien las calculadoras y los programas de hojas de cálculo como las hojas de Excel tienen funciones integradas para calcular con precisión el tiempo preciso requerido para duplicar el dinero invertido, la Regla del 72 es útil para que los cálculos mentales estimen rápidamente un valor aproximado. Alternativamente, puede calcular la tasa anual de rendimiento compuesto de una inversión dada la cantidad de años que se necesitarán para duplicar la inversión.

CONSEJOS CLAVE

• La regla del 72 es una forma simplificada de estimar la duplicación del valor de una inversión, basada en una fórmula logarítmica.
• La Regla del 72 se puede aplicar a inversiones, inflación o cualquier cosa que crezca, como el PIB o la población.
• La fórmula es útil para comprender el efecto del interés compuesto.

La fórmula para la regla del 72 es

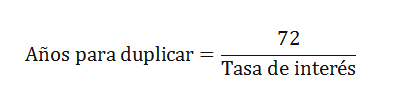
dónde:
Tasa de interés = Tasa de rendimiento de una inversión

Cómo calcular la regla del 72

Si un plan de inversión promete una tasa de rendimiento compuesta anual del 8%, se necesitarán aproximadamente (72/8) = 9 años para duplicar el dinero invertido. Tenga en cuenta que un rendimiento anual compuesto del 8% se inserta en esta ecuación como 8, y no como 0,08, lo que da un resultado de nueve años (y no de 900).

La fórmula ha surgido como una versión simplificada del cálculo logarítmico original que involucra funciones complejas como tomar el logaritmo natural de números. La regla se aplica al crecimiento exponencial de una inversión basada en una tasa de rendimiento compuesta.

La fórmula precisa para calcular el tiempo exacto de duplicación de una inversión que genera una tasa de interés compuesta de r% por período es la siguiente:

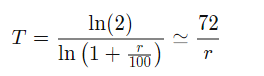
dónde:
T = tiempo para duplicar
ln = función logarítmica natural
r = Tasa de interés compuesta por período
≃ = Aproximadamente igual a

Para saber exactamente cuánto tiempo tomaría duplicar una inversión que rinde un 8% anual, usaría la siguiente ecuación:

• T = ln (2) / ln (1 + (8/100)) = 9.006 años, que es muy cercano al valor aproximado obtenido por (72/8) = 9 años

Dado que las personas no pueden hacer funciones logarítmicas instantáneamente sin la ayuda de tablas de registro o calculadoras científicas, pueden confiar en la versión más simple que usa el factor 72 y obtiene casi el mismo resultado. Si se necesitan 9 años para duplicar una inversión de $ 1,000, entonces la inversión aumentará a $ 2,000 en el año 9, $ 4,000 en el año 18, $ 8,000 en el año 27, y así sucesivamente.

¿Qué te dice la regla del 72?

A la gente le encanta el dinero, y les encanta más ver que el dinero se duplica. Obtener una estimación aproximada de cuánto tiempo llevará duplicar el dinero también ayuda al ciudadano medio a comparar inversiones. Sin embargo, los cálculos matemáticos pueden ser complejos para que las personas comunes calculen cuánto tiempo se requiere para que su dinero se duplique a partir de una inversión particular que promete una cierta tasa de rendimiento. La Regla del 72 ofrece un atajo útil ya que las ecuaciones relacionadas con el interés compuesto son demasiado complicadas para que la mayoría de las personas las prescindan sin una calculadora.

Interés simple versus compuesto

La tasa de interés que se cobra por una inversión o un préstamo se divide en dos categorías: simple o compuesta. El interés simple se determina multiplicando la tasa de interés diaria por el monto principal y por el número de días que transcurren entre los pagos. Se utiliza para calcular los intereses de las inversiones en las que el interés acumulado no se agrega al capital.

En el caso del interés compuesto, el interés se calcula sobre el principal inicial y también sobre el interés acumulado de períodos anteriores de un depósito. El interés compuesto se puede considerar como “interés sobre interés” y hará que el dinero invertido crezca a una cantidad mayor a una tasa más rápida en comparación con el interés simple, que se calcula solo sobre la cantidad principal.

En pocas palabras, dado que la porción de interés se acumula en el caso del interés compuesto, aumenta el valor principal con cada mes que pasa y conduce a rendimientos exponenciales más altos en general. Al no retirar los intereses todos los meses, el inversor aumenta el valor del capital, lo que le ayuda a ganar más intereses.

Contrasta con el interés simple en el que el inversor retira el interés todos los meses y mantiene constante el monto del capital, lo que genera rendimientos comparativamente más bajos. La Regla del 72 se aplica a los casos de interés compuesto y no a los de interés simple.

Ejemplos de cómo usar la regla del 72

La unidad no necesariamente tiene que invertirse o prestarse dinero. La Regla del 72 podría aplicarse a cualquier cosa que crezca a una tasa compuesta, como población, cifras macroeconómicas, cargos o préstamos. Si el producto interno bruto (PIB) crece al 4% anual, se espera que la economía se duplique en 72 ÷ 4 = 18 años.

Con respecto a la tarifa que se come las ganancias de inversión, la Regla del 72 se puede utilizar para demostrar los efectos a largo plazo de estos costos. Un fondo mutuo que cobra un 3% en tarifas de gastos anuales reducirá el capital de la inversión a la mitad en unos 24 años. Un prestatario que paga 12% de interés en su tarjeta de crédito (o cualquier otra forma de préstamo que cobre interés compuesto) duplicará la cantidad que adeuda en seis años.

La regla también se puede utilizar para encontrar la cantidad de tiempo que tarda el valor del dinero en reducirse a la mitad debido a la inflación. Si la inflación es del 6%, entonces un determinado poder adquisitivo del dinero valdrá la mitad en aproximadamente (72 ÷ 6) = 12 años. Si la inflación disminuye del 6% al 4%, se espera que una inversión pierda la mitad de su valor en 18 años, en lugar de 12 años.

Además, la Regla del 72 se puede aplicar en todo tipo de duraciones siempre que la tasa de rendimiento sea compuesta. Si el interés por trimestre es del 4%, entonces se necesitarán (72/4) = 18 trimestres o 4,5 años para duplicar el capital. Si la población de una nación aumenta a una tasa del 1% mensual, se duplicará en 72 meses o seis años.

Variaciones en la aplicación de la regla del 72

La Regla del 72 es razonablemente precisa para las tasas de interés que caen en el rango del 6% y el 10%. Cuando se trata de tasas fuera de este rango, la regla se puede ajustar sumando o restando 1 de 72 por cada 3 puntos que la tasa de interés difiera del umbral del 8%. Por ejemplo, la tasa de interés compuesto anual del 11% es 3 puntos porcentuales superior al 8%.

Por lo tanto, agregar 1 (para los 3 puntos superiores al 8%) a 72 lleva a usar la regla del 73 para una mayor precisión. Para una tasa de rendimiento del 14%, sería la regla del 74 (sumando 2 por 6 puntos porcentuales más alta), y para una tasa de rendimiento del 5%, significará reducir 1 (por 3 puntos porcentuales más baja) para llevar a la regla de 71.

Por ejemplo, supongamos que tiene un plan de inversión muy atractivo que ofrece una tasa de rendimiento del 22%. La regla básica de 72 dice que la inversión inicial se duplicará en 3,27 años. Sin embargo, dado que (22 – 8) es 14 y (14 ÷ 3) es 4,67 ≈ 5, la regla ajustada debe usar 72 + 5 = 77 para el numerador. Esto da un valor de 3.5 años, lo que indica que tendrá que esperar un cuarto adicional para duplicar su dinero en comparación con el resultado de 3.27 años obtenido de la regla básica del 72. El período dado por la ecuación logarítmica es 3.49, por lo que el El resultado obtenido de la regla ajustada es más preciso.

Para la composición diaria o continua, el uso de 69,3 en el numerador da un resultado más preciso. Algunas personas ajustan esto a 69 o 70 para facilitar los cálculos.

En medio de todas las variaciones sugeridas para mejores estimaciones, uno puede confiar en la Regla básica del 72 para hacer el cálculo mental rápido para evaluar aproximadamente cuándo se duplicaría su dinero o el monto del préstamo.