Las aplicaciones de blockchain de teoría de juegos pueden ayudarlo a comprender cómo funcionan los sistemas criptoeconómicos descentralizados sin ser víctimas de la desintegración interna y las trampas. La teoría de juegos es un estudio de modelos matemáticos de interacción estratégica y toma de decisiones entre tomadores de decisiones racionales.

Si bien la teoría de juegos puede ser tanto cooperativa como no cooperativa, nos centraremos exclusivamente en esto último, ya que un entorno criptoeconómico descentralizado es, por diseño, sin confianza y no cooperativo.

Su modelo típico de teoría de juegos tiene tres componentes:

• Jugadores: los que toman todas las decisiones. P.ej. La junta directiva de una empresa.
• Estrategias: las decisiones que tomará la empresa para promover su agenda.
• Pago: Resultado de las estrategias que han realizado los jugadores.

Diseñada por primera vez por John von Neumann y Osker Morgenstern en 1944, la teoría de juegos fue un avance significativo en el estudio de los mercados de oligopolios.

¿Qué es el oligopolio?

La estructura del mercado son las características organizativas y fundamentales de un mercado en particular. Con base en una variedad de factores diferentes, como el número de productores, el control de los precios y las barreras de entrada, estas estructuras se dividen en las siguientes cuatro categorías:

• Competencia perfecta
• Monopolio
• Competencia monopolística
• Oligopolio.

competencia perfecta

Imagínese el puesto de limonada de su hijo.

Este es un ejemplo de competencia perfecta. Cualquiera puede ingresar al mercado y los vendedores individuales no tienen ningún poder sobre el precio del producto. Si el pequeño Johnny decide subir el precio de su limonada a 30 centavos, sus clientes simplemente acudirán a Mary, que vende la suya por 25 centavos.

Monopolio

El polo opuesto de una estructura de mercado de “competencia perfecta” es la estructura de monopolio. En un monopolio, una entidad domina el mercado. La barrera de entrada es a menudo tan alta que, de todos modos, no es factible que alguien nuevo entre en el mercado.

Piense en Xerox. ¿Existe un mejor ejemplo de sector monopolista que el espacio de “fotocopias”? De manera similar, De Beers es otro ejemplo de una empresa que tiene el monopolio de su mercado: los diamantes.

Competencia monopolística

La competencia monopolística es un mercado que tiene muchos vendedores y una barrera de entrada poco profunda. Los productos vendidos por los competidores también son similares pero no idénticos. Piense en la industria de las donas. Tenemos Dunkin Donuts, Krispy Kreme, Tim Hortons, etc. Todos ellos tienen un producto que se asemeja a ligeras diferencias sutiles en sabor y apariencia.

Por lo general, sus productos se encuentran aproximadamente en el mismo rango de precios y no tienen mucho margen de maniobra. Si Dunkin Donuts comienza a cobrar de más, la gente simplemente irá a Krispy Kreme o Tim Hortons. Si los tres comienzan a cobrar de más, un nuevo jugador puede ingresar al mercado debido a la baja barrera de entrada.

Oligopolio

Los oligopolios son similares a la competencia monopolística pero con una pequeña diferencia. Las barreras de entrada en un oligopolio son increíblemente altas.

Uno de los mejores ejemplos de oligopolio es el mercado de relojes de pulsera de alta gama. Empresas como Rolex, Breitling, Patek Philippe, etc., dominan este mercado. Los productos son similares pero no idénticos. Sin embargo, esto no les da un control total sobre el mercado. P.ej. Si Rolex dispara el precio de su modelo Submariner a $ 10,000, solo los fanáticos de Rolex se quedarán con la compañía. Todos los demás irán por alguna otra marca.

¿Cómo pueden estos productos incrementar el precio de sus productos sin perder a sus clientes frente a la competencia? Obviamente, pueden reunirse y planear aumentar el precio de los productos en su conjunto. Sin embargo, se supone que esto es altamente ilegal.

La única opción que tienen es la teoría de juegos.

La necesidad de la teoría de juegos

La economía clásica no tiene en cuenta la competencia imperfecta. La teoría de juegos te permite modelar comportamientos competitivos entre diferentes agentes. Las empresas generalmente enfrentan múltiples elecciones estratégicas que afectan su producción general. Es posible que tengan que tomar decisiones con respecto a:

• Detener la producción de un producto existente.
• Desarrollando un nuevo producto.
• Bajar el precio de un producto en relación con la competencia.
• Empleando nuevas estrategias de marketing.

Como dijimos antes, las empresas no pueden simplemente reunirse y decidir cómo fijar el precio de sus productos, ya que eso sería una colusión. La única forma en que pueden competir de manera efectiva es a través de la competencia sin precios. La forma más reconocible de competencia no relacionada con los precios es la publicidad.

Entonces, creemos una matriz de pagos para saber si dos empresas, A y B, pueden beneficiarse de la publicidad o no.

Por lo tanto, tenemos dos opciones, anunciar o no publicitar. Según la información dada en nuestra matriz:

• Si una empresa hace publicidad y la otra no, la primera se beneficia mucho, mientras que la otra no.
• Si ambos se anuncian, ambos pueden ganar bastante.
• Al examinar esta matriz de pagos, podemos ver que a ambas empresas les interesa anunciarse. En el ejemplo anterior, (4,3) es nuestro equilibrio de Nash.

Qué … ¿Qué es el equilibrio de Nash?

El famoso matemático John Forbes Nash Jr ideó una solución para un juego no cooperativo que involucra a dos o más jugadores llamado “Equilibrio de Nash”. Sí, este es el mismo John F Nash, quien fue interpretado por Russell Crowe en la película “A Beautiful Mind”.

En una situación de juego no cooperativo, el equilibrio de Nash se considera la solución ideal para los dos participantes involucrados. En este estado, ambos tienen algo que ganar con la recompensa. Desviarse del equilibrio conducirá a una pérdida de pago para uno o ambos participantes.

Ahora que tenemos una breve idea de cómo funciona, veamos uno de los conceptos más conocidos en la teoría de juegos: El dilema del prisionero.

El dilema del prisionero

El Caballero de la Noche tuvo una escena emocionante hacia el final de la película. El Joker había manipulado dos transbordadores con explosivos. Un ferry estaba lleno de ciudadanos inocentes y el otro lleno de criminales. Cada nave tenía un controlador que voló a la otra. El Joker luego anunció esto:

Tendrán que volar la otra nave antes de un límite de tiempo determinado.
Si el límite de tiempo expira, entonces el Joker volará ambos barcos.
Este es un ejemplo clásico del juego “El dilema del prisionero”. La idea fue creada inicialmente por Merrill Flood y Melvin Dresher mientras trabajaban en RAND en 1950.

El dilema del prisionero es un escenario hipotético en el que dos individuos completamente racionales pueden no cooperar, incluso si lo mejor para ellos es hacerlo. En la película, tanto los prisioneros como los ciudadanos decidieron no volar el barco del otro en un ejemplo bastante conmovedor de la bondad innata de los seres humanos. Hicieron esto a pesar de que:

• No sabían si el otro barco los haría explotar o no.
• El Joker dijo que si ninguno de los barcos había explotado en el límite de tiempo dado, los volaría a ambos.
• Obviamente, no pasó nada porque Batman terminó salvando el día, pero en realidad, no puedes esperar que un multimillonario desgarrado con un disfraz de Halloween te impida tomar malas decisiones.

Entonces, pongamos este dilema bajo el microscopio con otro ejemplo.

Supongamos que arrestan a Alice y Bob por robar un banco. Actualmente, su interrogatorio se lleva a cabo en salas separadas. La policía les da las siguientes proposiciones:

• Si alguno de ellos no delata al otro, ambos recibirán 5 años de prisión.
• Sin embargo, si uno critica al otro, quedará libre de culpa mientras que el otro tendrá 7 años de prisión.
• Si ambos critican al otro, ambos reciben una sentencia de 3 años.
• La matriz de pagos de este escenario se ve así:

Idealmente hablando, tanto Alice como Bob no querrán confesarse. Sin embargo, la teoría de juegos nos dice que puede que no sea el escenario más realista. Tanto Alice como Bob se enfrentan a recompensas mucho mejores si delatan a la otra persona. Desde el punto de vista de Alice, ella obtiene:

• 0 años si Bob no confiesa.
• 3 años si Bob confiesa.

Ambas opciones son mucho mejores que los 5 años que tendrá si no confiesa. También corre el riesgo de recibir una sentencia de 7 años si Bob confiesa. Entonces, en este escenario, lo mejor para ambos es delatar a la otra persona. Por tanto, el equilibrio de Nash se encuentra en (3,3).

El dilema del prisionero con el factor castigo

Ahora, veamos la implicación moral del equilibrio. ¿Qué pasa si la rentabilidad óptima de una matriz es perjudicial para la sociedad? Considere la siguiente matriz de pagos. Alice y Bob están decidiendo si robar o no un banco:

La recompensa es mayor cuando Alice y Bob roban juntos porque será mucho más eficiente. Entonces, el equilibrio de Nash radica en que ambos roban el banco. Hmmm … esto no se ve bien. Si esta condición es válida para todas las matrices de pagos similares, ¿no caería nuestra sociedad en una locura total? Es por eso que nosotros, como sociedad, hemos introducido un factor de “castigo” para mitigar este caos.

¿Cómo funciona el castigo?

A diferencia de lo que sucedió en The Dark Knight, es posible que las personas no siempre elijan hacer lo correcto. Los seres humanos, lamentablemente, son propensos a la corrupción. Implementar un factor de castigo a las recompensas ayudará a mantener a la sociedad bajo control.

En el ejemplo anterior, imaginemos que el factor de castigo funciona así:

“Por cada acción que se tome contra el interés público, se le dará un factor de castigo de -7”.

Ahora nuestra matriz de pagos se ve así. La recompensa de cada acción dañina se reduce en un factor de 7:

Las recompensas ahora han cambiado considerablemente. Gracias a nuestro factor de castigo, lo mejor para Alice y Bob es no robar, y (1,1) se convierte en nuestro Equilibrio de Nash.

El punto de Schelling

Piense en un pub popular en su ciudad donde la gente va a relajarse después de un día agotador en el trabajo. Lo más probable es que simplemente te encuentres con tus amigos y colegas en el bar. No es necesario enviarles un mensaje de texto de antemano para coordinar. Esto se debe a que la barra resulta ser un punto de Schelling para sus colegas.

Entonces, ¿qué es un punto de Schelling? Es una solución que la gente utilizará automáticamente en ausencia de una comunicación adecuada. La respuesta suele ser un valor que es especial para ellos y se siente natural / distinto.

Entendamos esto con otro ejemplo. Supongamos que tenemos dos personas en dos habitaciones diferentes. Ambos tienen que pasar por una serie de números y adivinar qué elegirá la otra persona. Los números dados son: 7241, 5467, 1 y 8723.

¿Qué número crees que es más probable que elijan? Probablemente “1”, ¿verdad? Se siente natural elegirlo, ya que es bastante diferente a los otros números que se dan en la lista.

Racionalidad limitada

El siguiente concepto que vamos a analizar es el de racionalidad limitada. Considere este ejemplo.

Vas a la tienda de comestibles todos los días y compras una manzana. Lo hiciste todos los días sin falta, como un ritual. Sin embargo, cada vez que lo haces, te enfrentas a un escenario extraño. Todos los días, durante un par de minutos, el comerciante se va para terminar un mandado. La tienda es bastante de la vieja escuela, por lo que no tiene ninguna cámara de seguridad en su lugar. Puedes robar fácilmente una manzana y nadie se enterará.

Sin embargo, no haces eso. Este es un ejemplo de racionalidad limitada.

La racionalidad limitada establece que la racionalidad de nuestras decisiones estará dentro de los límites de la información disponible para nosotros y nuestra capacidad mental.

En términos simples, las personas siempre van a tomar decisiones que les son naturales y no requieren muchas complicaciones. Ahora, tenga en cuenta que “simple” no siempre significa “correcto”. La decisión no tiene por qué producir las recompensas más altas, y puede que no sea la más adecuada para ellos, pero aún así es algo que les resultará natural.

Tomemos otro ejemplo de esto: el comercio de criptomonedas.

El mercado de las criptomonedas es muy volátil y hay demasiada información que procesar para un ser humano normal. Es casi imposible que alguien tome una decisión prudente y bien educada, dados varios límites de tiempo e intelectuales. La mayoría de las veces, las personas se basan en experiencias previas o en el juicio de otra persona en la que confían.

En lugar de tener en cuenta todos los diferentes factores y tomar una decisión super educada que afecte positivamente sus ingresos, la mayoría de los inversores simplifican su toma de decisiones y obtienen un resultado óptimo, que puede que no sea el mejor. Por tanto, el comercio es un ejemplo de racionalidad limitada.

Equilibrio del gatillo sombrío

El siguiente concepto que vamos a analizar es el “Equilibrio del desencadenante sombrío”. En la antigüedad, una de las reglas más comunes en vigor era el “derecho divino de los reyes”. La gente creía que ciertos individuos y sus familias son elegidos por los dioses para gobernar a las masas. Como tal, el rey a menudo se considera un ser divino.

Ahora bien, ¿qué pasa si alguien asesina al rey a sangre fría?

Dado que la mortalidad del rey está expuesta, el derecho divino del rey desaparece. En el momento en que eso sucede, la sociedad entra en el caos. Una vez que el rey parece ser asesinado, comienza un ciclo interminable de derramamiento de sangre donde los futuros reyes siguen siendo asesinados por usurpadores o el público descontento.

La única forma de detenerlo es no comenzarlo en primer lugar. Al no matar al rey original, mantienes la idea de un “derecho divino”. A esto se le llama “Equilibrio de desencadenante sombrío”. Un Grim Tigger es un estado de equilibrio en el que una ligera desviación conduce a un ciclo interminable de castigo recursivo.

Juego de coordinación

Eche un vistazo a esta matriz:

A

B

A

(10,10)

(0,0)

B

(0,0)

(10,10)

Esta matriz tiene dos equilibrios de Nash: (A, A) y (B, B). Los dos jugadores pueden elegir cualquiera de ellos y aún así obtener la misma recompensa. Imaginemos también que (A, A) es la opción más popular por ahora. La pregunta es cómo movemos nuestro equilibrio de (A, A) a (B, B).

Este escenario particular es crítico para una WAN como Bitcoin. Un pequeño grupo de personas puede coordinarse fácilmente entre sí por teléfono y correo electrónico. Sin embargo, una red deliberadamente descentralizada como Bitcoin tendrá dificultades para coordinarse adecuadamente entre sí. Entonces, si hay una actualización en el sistema, ¿cómo nos aseguramos de que la comunidad pueda saltar de un protocolo a otro sin tener que conectarse entre sí individualmente?

La solución aquí es convencer a la mayoría de la red de que cambie el protocolo, mientras que el resto seguirá. Comprendamos cómo funciona esto con un ejemplo simple. Imagínese que hay una nueva aplicación de mensajería en el mercado. Si casi todos tus amigos pasan a la nueva aplicación, querrás descargarla también, ¿verdad? Después de todo, no querrá perderse la diversión.

La misma lógica también funciona para un protocolo descentralizado. Si la mayoría de la red avanza orgánicamente hacia el nuevo protocolo, el resto de los nodos eventualmente avanzará porque no quieren quedarse fuera del circuito.

Prueba de teoría de juegos de trabajo

Veamos cómo estos diferentes principios de la teoría de juegos mitigan los escenarios de ataque en una cadena de bloques. Una cadena de bloques es una serie de bloques vinculados que contienen datos con marca de tiempo.

La cadena de bloques de Bitcoin sigue un modelo de consenso llamado “prueba de trabajo”. En este modelo, tenemos ciertos participantes llamados mineros, que usan su poder computacional para minar en la cadena de bloques y crear nuevos bloques. Las diferencias entre una cadena de bloques y otras redes descentralizadas similares, como Tangle, se describen en el artículo Blockchain vs Tangle.

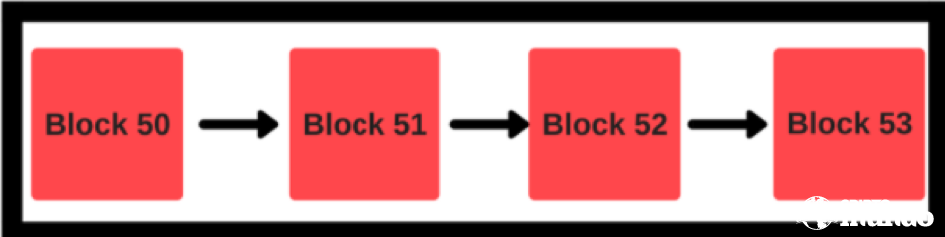
The structure that you see above is a more idealistic version of the blockchain. In reality, it looks more like this:

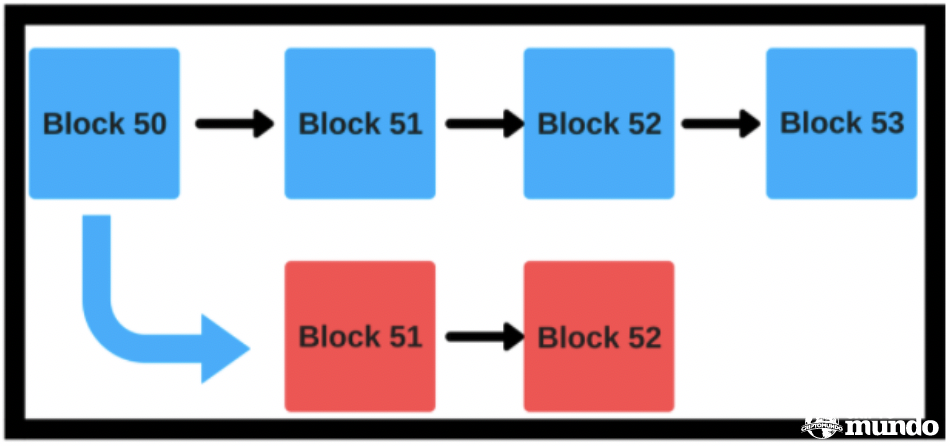
Hay decenas de miles de cadenas laterales adjuntas a la cadena de bloques principal de Bitcoin. Para evitar cualquier confusión y evitar el doble gasto, la mayoría de los mineros de Bitcoin no tienden a minar en estas cadenas laterales más pequeñas. La razón de esto es bastante simple. La cadena más larga de la red Bitcoin actúa como punto de Schelling para los mineros de Bitcoin. La minería en cualquiera de las otras cadenas laterales termina siendo un gran desperdicio de recursos, ya que las transacciones realizadas en esas cadenas no se consideran de valor real.

Sin embargo, el fundador de Ethereum, Vitalik Buterin, dio un ejemplo interesante de cómo alguien puede hacerse cargo de un sistema de prueba de trabajo. Si el atacante tiene enormes recursos y suficiente motivación, teóricamente puede hacerse cargo de una cadena de bloques de prueba de trabajo mediante el uso de un modelo de soborno o un “ataque P + Epsilon”.

Ataque P + Epsilon

Para comprender el ataque “P + Epsilon”, mire esta tabla. Imaginemos que es un minero y veamos cómo sus decisiones con respecto a los otros mineros cambian su recompensa:

Podemos sacar las siguientes conclusiones:

• Si toma la misma decisión que los otros mineros, obtendrá una recompensa.
• Si su decisión contradice la de los otros mineros, no obtendrá ninguna recompensa.

Hay dos equilibrios de Nash en la matriz anterior.

• Elegir permanecer en la cadena o ir a una cadena diferente requerirá una coordinación significativa.
• La teoría de la coordinación dice que una buena mayoría necesita pasar al siguiente estado para que el nuevo escenario / cadena funcione.

Supongamos ahora que tenemos un atacante con recursos considerables. Este atacante ingresa a la red y se acerca individualmente a los mineros individuales. Les dice que si votan de manera diferente al sistema, obtendrán una recompensa de “P + ε”. La recompensa habitual y un soborno extra de ε además de eso. Ahora, nuestra matriz se ve así:

Ahora, esto lleva a otra situación inusual:

• Si eliges quedarte, hay una probabilidad de 50 a 50 de que obtengas una recompensa.
• Si elige ir en una cadena diferente, obtendrá una recompensa P o una recompensa de P + ε, dependiendo de lo que hayan elegido otros.

Obviamente, tomará una decisión que garantice alguna recompensa. Por lo tanto, elegirá ir a una cadena diferente.

Ahora supongamos que este atacante se ha acercado a todos los mineros con este trato, entonces sucede algo fascinante. Dado que todos votan para ir en una cadena diferente, el equilibrio de Nash cambia a:

Entonces, el atacante pudo cambiar todo el curso de la red sin necesidad de pagar ese soborno adicional.

¿Cómo puede la teoría de juegos mitigar el escenario anterior?

Como ya se mencionó, los mineros tienen un incentivo económico para minar en la cadena más larga porque es el Punto Schelling de toda la red.

Los usuarios valorarán más la cadena principal ya que simplemente están acostumbrados a ella. Al igual que los estados de racionalidad limitada, las personas optarán por la solución más simple en todo momento. Pasar por una cadena más nueva complica las cosas.

Sobornar a la red de esta manera cambiará el sombrío equilibrio del gatillo. ¿Qué impedirá que los futuros atacantes vuelvan a sobornar al sistema para que cambie a una cadena más nueva? Para evitar este sistema de castigo recursivo, es mucho mejor no cambiar el enfoque de la cadena principal original en primer lugar.

Finalmente, especialmente en el contexto de la cadena de bloques de Bitcoin, la red es tan vasta y descentralizada, que no es factible que un soborno se conecte individualmente con la mayoría de los mineros en un intento de organizar un golpe de coordinación. Resolver este problema de coordinación requiere una cantidad absurda de ingenio, impulso y paciencia por parte del atacante.

Conclusión

La teoría de juegos previene la corrupción interna y ayuda en la toma de decisiones racional para los oligopolios y otras estructuras económicas. Es el corazón y el alma de todos los sistemas financieros y criptoeconómicos y es uno de los factores más importantes para mantener su integridad general. Aquellos interesados ​​en la mecánica de la cadena de bloques de la teoría de juegos deben asegurarse de examinar también el problema de los generales bizantinos.